How to Calculate Miter Saw Angle?

The miter saw angle is essential for perfect workpiece joints. Miter saw angle depends on the joint angle and workpiece width; due to the various angles and lengths it’s unable to calculate quickly. So let’s see how to calculate the miter saw angles in a few steps.

A miter saw angle depends on the joint angle and workpiece width. If you need to calculate the miter saw angle, you will need a bit of depth of knowledge about trigonometry functions. It is easy. So let’s see how to calculate the miter saw angle quickly.

Mathematical Steps to Find Miter Saw Angle

So, let’s prove a common equation by using workpiece widths and angles to be cut.

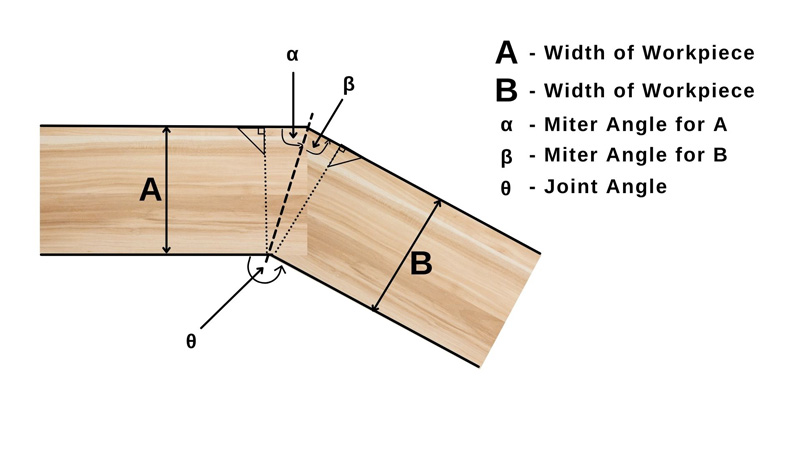
Eqn 01 ↦  α+β=θ
X - Face Length

Using Sin Low
Sinα = A∕X       Sinβ=B∕X  

Hence, 
Eqn 02 ↦ A∕Sinα = B/Sinβ

α+β=θ Can be written as below

α=θ-β
Hence, 
Eqn 03 ↦Sinα = Sin(θ-β)

From Eqn 02 , and Eqn 03;

Sin(θ-β) = A*Sinβ/B

Expanding Sin(θ-β)

SinθCosβ-CosθSinβ = A*Sinβ/B

Divide both sides from (÷Sinβ)

SinθCotβ-Cosθ = A/B

Cotβ = (A/B + Cosθ ) /Sinθ

Tanβ = Sinθ/ (A/B + Cosθ ) 

β = Arctan(Sinθ/ (A/B + Cosθ ) )
α = θ-β

After you get the angles for α and β, it will not be the miter angle. It is the angle you have to keep in your workpiece. So you need the angle to be removed.

This can be calculated by reducing 90 degrees.

So, let’s see how to do it.

**Trigonometric Tables For Sin, Cos, Tan Values

Read more about – Miter saw Parts and Functions

Calculating Miter Angle for 120 Degrees for 8cm and 12cm Workpiece Joints

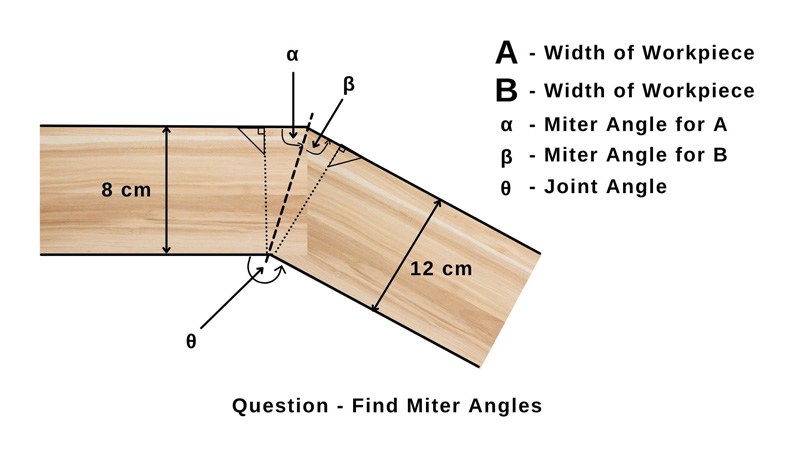
Calculate the miter angle for joining angle θ = 120 and workpiece width 8cm and 12cm.

Eqn 01 ↦  α+β=120
X - Face Length

Using Sin Low
Sinα = 8∕X       Sinβ=12∕X  

Hence, 
Eqn 02 ↦ 8∕Sinα = 12/Sinβ

α+β=120 Can be written as below

α=120-β
Hence, 
Eqn 03 ↦Sinα = Sin(120-β)

From Eqn 02 , and Eqn 03;

Sin(120-β) = 8*Sinβ/12

Expanding Sin(θ-β)

Sin120Cosβ-Cos120Sinβ = 8*Sinβ/12

Divide both sides from (÷Sinβ)

Sin120Cotβ-Cos120 = A/B

Cotβ = (8/12 + Cos120 ) /Sin120

Tanβ = Sin120/ (8/12 + Cosθ120 ) 

β = Arctan(Sin120/ (8/12 + Cos120 ) )
β = Arctan(0.866/(8/12 - 0.5)
β = Arctan(5.1)

β = 78.90
α = θ-β

α = 120-78.90
α = 41.1

Hence Miter Angle for 8 cm workpiece = 90 – 41.1 = 48.9 Degree

Hence Miter Angle for 8 cm workpiece = 90 – 78.90= 11.1 Degree